Cheat sheet on Neural Networks 1¶
The following article is a cheat sheet on neural networks. My sources are based on the following course and article:
- the excellent Machine Learning course on Coursera from Professor Andrew Ng, Stanford,
- the very good article from Michael Nielsen, explaining the backpropagation algorithm.
Why the neural networks are powerful ?¶
It is proven mathematically that:
Suppose we’re given a [continuous] function f(x) which we’d like to compute to within some desired accuracy ϵ>0. The guarantee is that by using enough hidden neurons we can always find a neural network whose output g(x) satisfies: |g(x)−f(x)|<ϵ, for all inputs x.
Michael Nielsen — From the following article
Conventions¶
Let’s define a neural network with the following convention:
L = total number of layers in the network.
$s_l$ = number of units (not counting bias unit) in layer l.
K = number of units in output layer ( = $s_L$ ).
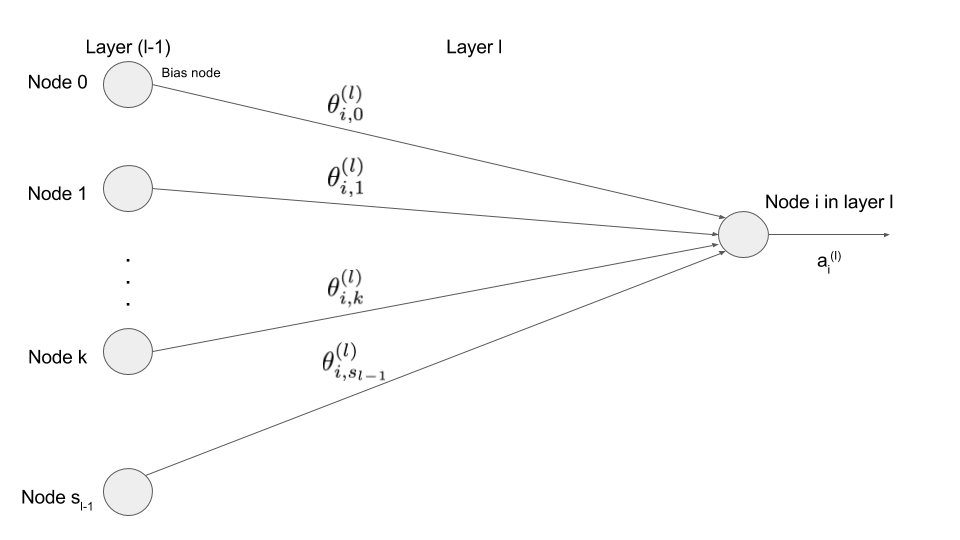
With:
$$ \forall l \in\ {2, ..., L-1},\ a^{(l)} \in \mathbb{R}^{s_{l}+1} and\ \begin{cases} a^{(l)}_0\ =\ 1\ (bias\ node)\\ a^{(l)}_i = g(z^{(l)}_i), \forall i \in {1, ..., s_l}\\ \end{cases}\\ z^{(l)}_i = [ \theta^{(l)}_i ]^T . a^{(l-1)}, \forall i \in {1, ..., s_l}\\ with\ \theta^{(l)}_i \in \mathbb{R}^{s_{l-1}+1}\ and\ z^{(l)} \in \mathbb{R}^{s_{l}}\ $$We define the matrix θ of the weights for the layer l as following:
$$ \theta^{(l)} \in \mathbb{R}^{s_l \times (s_{(l-1)}+1)} $$$$ \theta^{(l)} = \begin{bmatrix} [ \theta^{(l)}_1 ]^T \\ [ \theta^{(l)}_2 ]^T \\ \vdots \\ [ \theta^{(l)}_{s_{l}} ]^T \end{bmatrix} = \begin{bmatrix} \theta_{1,0} & \dots & \theta_{1,j} & \dots & \theta_{1,s_{l-1}} \\ \vdots & & \vdots & & \vdots \\ \theta_{i,0} & \dots & \theta_{i,j} & \dots & \theta_{i,s_{l-1}} \\ \vdots & & \vdots & & \vdots \\ \theta_{s_l,0} & \dots & \theta_{s_l,j} & \dots & \theta_{s_l,s_{l-1}} \\ \end{bmatrix} $$Hence, we have the following relation: $$ a^{(l)} = \left(\begin{smallmatrix}1 \\ g(\theta^{(l)}.a^{(l-1)})\end{smallmatrix}\right) \tag{0} $$
The cost function of a Neural Network¶
The training set is defined by: $ { (x^1,y^1), ..., (x^m,y^m) } $
x and y are vectors, with respectively the same dimensions as the input and output layers of the neural network.
The cost function of a neural network is the following:
$$ J(\theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[ cost( a^{(L)}_k, y^{(i)}_k) \right] + \frac{\lambda}{2m}\sum_{l=2}^{L} \sum_{j=1}^{s_l} \sum_{i=1}^{s_{l+1}} ( \theta_{i,j}^{(l)})^2 $$$a^{(L)}_k$ is the output of the neural network, and is dependent of the weights 𝜃 of the neural network.
Please note that the regularization term does not include the weights of the bias nodes.
Now, the objective is to train the neural network and find the minimum of the cost function J(𝜃).
Mathematic reminder: the chain rule¶
Let’s define the functions f, g and h as following:
$$ f:\mathbb{R}^n \rightarrow \mathbb{R} $$$$ g:\mathbb{R}^p \rightarrow \mathbb{R}^n $$$$ h = f \circ g $$The derivative of h is given by the chain rule theorem:
$$ \forall_i \in \{ \!1, ... , \!p \}, \frac{\partial h}{\partial x_i} = \sum_{k=1}^{n} \frac{\partial f}{\partial g_k} \frac{\partial g_k}{\partial x_i} $$(See the following course online on partial derivation from the MIT)
The backpropagation algorithm¶
We use the gradient descent to find the minimum of J on 𝜃: $ \min\limits_{\theta} J(\theta)$
The gradient descent requires to compute:
$$ \frac{\partial J(\theta)}{\partial \theta^{(l)}_{i,j}} $$In the following parts, we consider only the first part of J(θ) (as if the regularisation term λ=0). The partial derivative of the second term of J(θ) is easy to compute.
The following course from Andrej Karpathy gives an outstanding explaination how the partial derivatives works at the level of a node in the backpropagation algorithm.
Definition of ẟ¶
Let’s define the function ẟ. When ẟ of the layer l is multiplied by the output of the layer (l-1), we obtain the partial derivative of the cost function on θ.
Let’s use the chain rule and develop this derivative on z:
$$ \frac{\partial J(\theta)}{\partial \theta^{(l)}_{i,j}} = \sum^{s_l}_{k = 1} \frac{\partial J(\theta)}{\partial z^{(l)}_k} \frac{\partial z^{(l)}_k}{\partial \theta^{(l)}_{i,j}} $$(Remind that J is dependent of z)
As: $$z^{(l)}_k = [ \theta^{(l)}_k ]^T . a^{(l-1)} = \sum_{p=0}^{s_{l-1}} \theta^{(l)}_{k,p} \times a^{(l-1)}_p$$
$$\frac{\partial z^{(l)}_k}{\partial \theta^{(l)}_{i,j}} = 0\ for\ k\ ≠\ i\ and\ p\ ≠\ j\ in\ the\ sum.$$$$And\ \frac{\partial z^{(l)}_k}{\partial \theta^{(l)}_{i,j}} = a^{(l-1)}_j\ for\ k\ =\ i\ and\ p\ =\ j\ in\ the\ sum.$$We define the output error 𝛿: $$ \delta^{(l)}_k = \frac{\partial J(\theta)}{\partial z^{(l)}_k},\ \forall k \in {1, ..., s_l},\ and\ \delta^{(l)} = \nabla_{z^{(l)}} J(\theta) \in \mathbb{R}^{s_{l}} $$
So we have:
$$ \frac{\partial J(\theta)}{\partial \theta^{(l)}_{i,j}} = \delta^{(l)}_i . a^{(l-1)}_j $$
More specifically, for the derivatives of the bias node's weights, we have ($a^{(l)}_0 = 1,\ \forall l$):
$$ \frac{\partial J(\theta)}{\partial \theta^{(l)}_{i,0}} = \delta^{(l)}_i $$Value of ẟ for the layer L¶
Now let’s find 𝛿 for the output layer (layer L):
$$ \delta^L_i = \frac{\partial J(\theta)}{\partial z^{(L)}_i} = \sum^{s_{L}}_{k = 1} \frac{\partial J(\theta)}{\partial a^{(L)}_k} \frac{\partial a^{(L)}_k}{\partial z^{(L)}_i} $$As:
$$ a^{(l)}_k = g(z^{(l)}_k),\ \frac{\partial a^{(L)}_k}{\partial z^{(L)}_i} = 0\ if\ k\ ≠\ i $$Hence:
$$ \delta^L_i = \frac{\partial J(\theta)}{\partial a^{(L)}_i} \frac{\partial g(z^{(L)}_i)}{\partial z^{(L)}_i} = \frac{\partial J(\theta)}{\partial a^{(L)}_i} . g'(z^{(L)}_i) $$
Relationship of ẟ between the layer l and the layer (l-1)¶
Now, we try to find a relation between 𝛿 of the layer l and 𝛿 of the next layer (l+1):
$$ \delta^{(l)}_i = \frac{\partial J(\theta)}{\partial z^{(l)}_i} = \sum^{s_{l+1}}_{k = 1} \frac{\partial J(\theta)}{\partial z^{(l+1)}_k} \frac{\partial z^{(l+1)}_k}{\partial z^{(l)}_i} $$With:
$$ z^{(l+1)}_k = [ \theta^{(l+1)}_k ]^T . g(z^{(l)}_p) = \sum_{p=0}^{s_{l}} \theta^{(l+1)}_{k,p} \times g(z^{(l)}_p) $$And:
$$ \frac{\partial z^{(l+1)}_k}{\partial z^{(l)}_i} = \theta^{(l+1)}_{k,i} . g'(z^{(l)}_i)\ \ for\ p\ =\ i,\ else\ 0. $$Hence:
$$ \delta^{(l)}_i = \sum^{s_{l+1}}_{k = 1} \delta^{(l+1)}_k . \theta^{(l+1)}_{k,i} . g'(z^{(l)}_i) $$
The meaning of this equation is the following:
The backpropagation algorithm explained¶
We have the following:
- we have found a function ẟ for the layer l such that when we multiply this function by the output of the layer (l-1), we obtain the partial derivative of the cost function J on the weights θ of the layer l,
- the function ẟ for the layer l has a relation with ẟ of the layer (l+1),
- as we have a training set, we can compute the values of ẟ for the layer L.
So, we start to compute the values of ẟ for the layer L. As we have a relation between ẟ for the layer l and ẟ for the layer (l+1), we can compute the values for the layers (L-1), (L-2), …, 2.
We can then compute the partial derivative of the cost function J on the weights θ of the layer l, by multiplying ẟ for the layer l by the output of the layer (l-1).
The vectorized backpropagation’s equations¶
The first equation gives the partial derivatives of J with respect to θ. We have added the regularization term.
$$ \nabla_{\theta^{(l)}} J(\theta) = \begin{bmatrix} \frac{\partial J}{\partial \theta^{(l)}_{1,0}} & \dots & \frac{\partial J}{\partial \theta^{(l)}_{1,j}} & \dots & \frac{\partial J}{\partial \theta^{(l)}_{1,s_{l-1}}} \\ \vdots & & \vdots & & \vdots \\ \frac{\partial J}{\partial \theta^{(l)}_{i,0}} & \dots & \frac{\partial J}{\partial \theta^{(l)}_{i,j}} & \dots & \frac{\partial J}{\partial \theta^{(l)}_{i,s_{l-1}}} \\ \vdots & & \vdots & & \vdots \\ \frac{\partial J}{\partial \theta^{(l)}_{s_l,0}} & \dots & \frac{\partial J}{\partial \theta^{(l)}_{s_l,j}} & \dots & \frac{\partial J}{\partial \theta^{(l)}_{s_l,s_{l-1}}} \\ \end{bmatrix} = \delta^{(l)} \otimes [a^{(l-1)}]^T + \frac{\lambda}{m} \theta^{(l)}_{zero\ bias} \tag{1} $$With $\theta^{(l)}_{zero\ bias}$ is $\theta^{(l)}$ with $\theta^{(l)}_{i,0}\ =\ 0,\ \forall i \in {1, ..., s_l}$ (the regularization term does not include the bias node's weights).
The second equation gives the relation between ẟ in layer l and ẟ in layer (l+1):
$$ \delta^{(l)} = [(\theta^{(l+1)}_{remove\ bias})^T . \delta^{(l+1)}] \odot g'(z^l) \tag{2} $$With $\theta^{(l)}_{remove\ bias}$ is $\theta^{(l)}$ with the column of the bias nodes' weights removed.
The third equation gives the value of ẟ for the layer L:
$$ \delta^{(L)} = \nabla_{a^{(L)}} J(\theta) \odot g'(z^L) \tag{3} $$Conclusion¶
This cheat sheet explains the backpropagation algorithm used to train a neural network. I have created this article after following the great Machine Learning’s course of Professor Andrew Ng on Coursera. The conventions used in this article are not exactly the ones used in the course of Professor Ng, nor exactly the ones used in the article of Michael Nielsen.
If you notice any error, please do not hesitate to contact me.